STEM 小知识: 奇特的斐波那契数
- Sahaana V
- 20. Juli 2020
- 2 Min. Lesezeit
你认为你知道关于斐波那契数的一切吗?看看这个吧!
你一定听说过斐波那契数。它们在自然界中经常出现,令人惊讶。例如,一朵花的花瓣数总是斐波那契数。
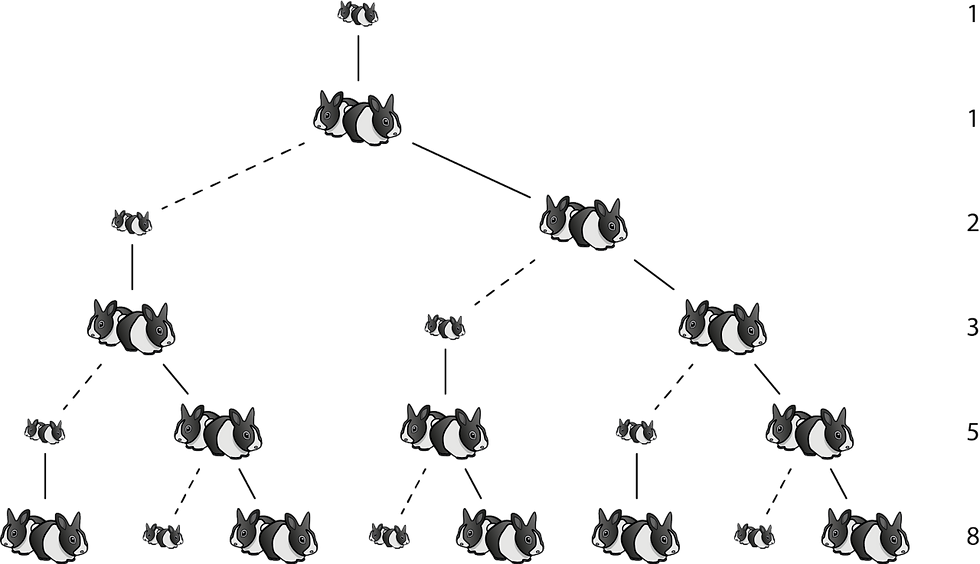
斐波纳契数列出现在斐波纳契本人所写的《Liber Abaci》一书中,以推广印度-阿拉伯数字系统的使用,取代罗马系统。它是作为以下问题的解决方案提出的:"某个人把一对兔子放在一个被墙包围的地方。如果假定每个月每对兔子[繁衍]一对新的兔子,从第二个月开始产出,那么这对兔子在一年中可以繁衍出多少对?" 答案是什么?斐波那契数字!
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
这些数字形成了几个模式。
假设,我们将1,1,2,3,5,8这一系列的数字进行平方。
我们得到 - 1, 1, 4, 9, 25, 64.....
现在,如果我们加上1+1,我们得到2,4+1,我们得到5,9+4我们得到13。因此,我们得到了系列的交替数字!
如果我们将这些方块相加,我们得到-- 1 + 1 = 2 1 + 1 + 4=6 1 + 1 + 4 + 9 = 15 ,等等. 因此,2=1*2,6=2*3,15=3*5,这些因素都进入了斐波那契数列中!
现在,这些模式的形成是有原因的。我们知道,-
1^1 + 1^1 + 2^2 + 3^2 + 5^2 = 40 = 8 × 5
如果放到1个大盒子里,比如下面给出的盒子,我们找到面积,我们会得到什么?我们得到了上面的数列!

如果我们从8开始用第二个数字除以第一个数字,例如--
104 = 13 * 8
273 = 13 * 21
13 ÷ 8 = 1.625
21 ÷ 13 = 1.615
34 ÷ 21 = 1.619
而黄金分割率或Phi大约是1.618! Phi或黄金比例是一个非常特殊的数字。读过《达芬奇密码》的人肯定听说过它。斐氏指数随处可见。眼睛和眼白之间的空间是黄金比例,你的前臂和手的比例是黄金比例,DNA螺旋有披的比例,向日葵中心的种子头,以及其他更多的有趣现象。
图片来自:
Google Images (Bunny image)
Translated into Mandarin by Han Yuyi







