Dose of STEM: Quirky Fibonacci Numbers

Think you know everything about Fibonacci numbers? Check this out!

You must have heard of the Fibonacci numbers. They occur in nature surprisingly often. For example, the number of petals in a flower is always a Fibonacci number.

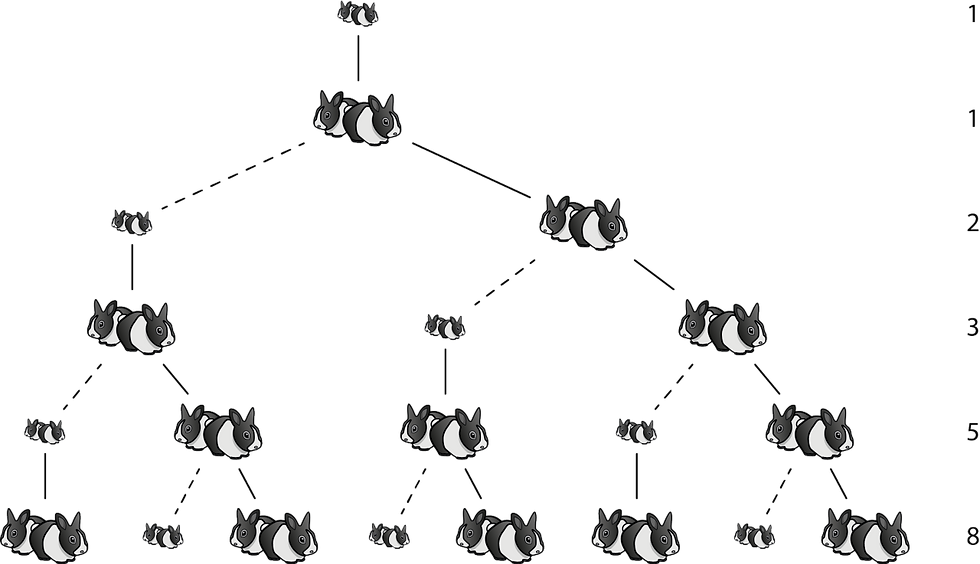
The Fibonacci sequence of numbers appeared in the book "Liber Abaci" written by Fibonacci himself, with an aim spread the usage of the Hindu-Arabic number system to replace the Roman system. It was presented as a solution to the following problem: "A certain man put a pair of rabbits in a place surrounded by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair [produces] a new pair which from the second month on becomes productive?" The solution to the problem can be provided by Fibonacci numbers.

The series: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

These Fibonacci numbers form several patterns which blow one's mind. Suppose, we square the numbers of the series 1, 1, 2, 3, 5, 8... , we get - 1, 1, 4, 9, 25, 64..... and so on. Now, if we add the next number in the series to the previous number, we get the alternate numbers of the series! For example, if we add 1 + 1, we get 2; if we add 4 + 1 and we get 5, and if we add 9 + 4 we get 13 — all of which are alternate numbers in the series. Building upon the squares, if we add all the squares and try to find the factors, we get - 1 + 1 = 2 = 1 * 2 1 + 1 + 4 = 6 = 2 * 3 1 + 1 + 4 + 9 = 15 = 3 * 5 , and so on. and these factors come into the Fibonacci series! Now, there is a reason these patterns are formed. We know that 1^1 + 1^1 + 2^2 + 3^2 + 5^2 = 40 = 8 × 5. If create a box such as the one given below, and find the area, we get the Fibonacci series.

There is another intriguing pattern that can be found while playing with Fibonacci numbers. If the second number is divided by the first number from the number 8 onwards, we get - 13 ÷ 8 = 1.625 21 ÷ 13 = 1.615 34 ÷ 21 = 1.619 and it is known that the golden ratio or phi is approximately 1.618! Phi or the golden ratio is a very special number; it is a mathematical ratio that can be found everywhere in nature. Spaces between eyes and the eye whites are in the golden proportion, the ratio of the forearm to the hand is in the golden ratio, DNA spirals have phi proportion, seed heads in the centre of a sunflower and this list can go on forever. The golden ratio makes things aesthetically pleasing and in fact, according to a study, our brains are hardwired to prefer things that have the golden ratio.

Do you know any other patterns formed by the Fibonacci series? Comment down below!

Image Source:

Google Images (Bunny image)