Dose de STEM: Chiffres de Fibonacci bizarres
- Sahaana V
- 21 июл. 2020 г.
- 2 мин. чтения
Vous pensez tout savoir sur les nombres de Fibonacci ? Regardez ça !
Vous avez sûrement entendu parler des nombres de Fibonacci. Ils apparaissent étonnamment souvent dans la nature. Par exemple, le nombre de pétales d'une fleur est toujours un nombre de Fibonacci.
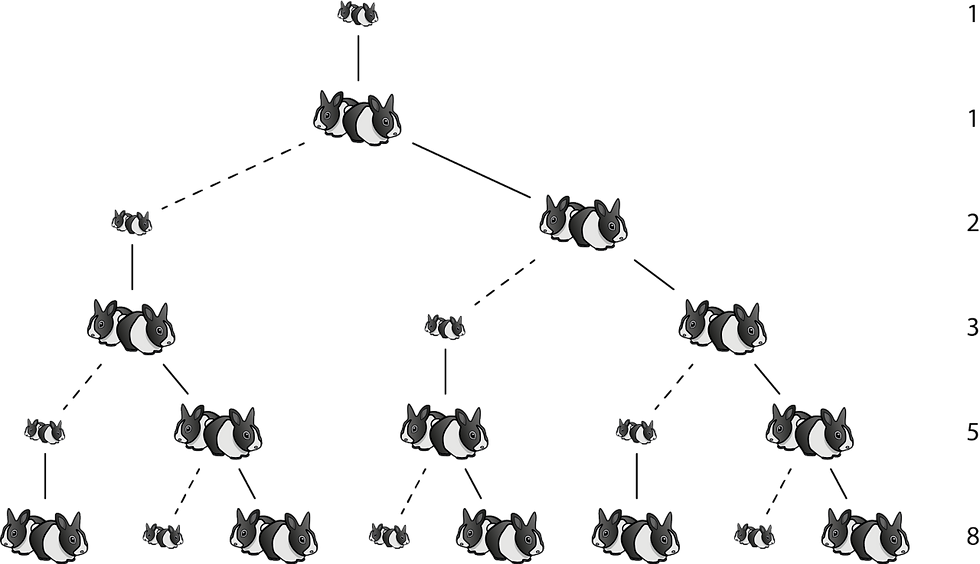
La suite des nombres de Fibonacci est apparue dans le livre "Liber Abaci" écrit par Fibonacci lui-même, afin de répandre l'usage du système numérique hindou-arabe pour remplacer le système romain. Elle était présentée comme une solution au problème suivant : "Un certain homme a placé une paire de lapins dans un endroit entouré d'un mur. Combien de paires de lapins peuvent être produites à partir de cette paire en un an, si l'on suppose que chaque mois, chaque paire [produit] une nouvelle paire qui, à partir du deuxième mois, devient productive ?" La solution ? Les nombres de Fibonacci !
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Ces nombres forment plusieurs modèles qui sont époustouflants.
Supposons que nous élevions au carré les nombres de la série 1, 1, 2, 3, 5, 8...
Nous obtenons - 1, 1, 4, 9, 25, 64.....
Maintenant, si on ajoute 1 + 1, on obtient 2, 4 + 1 et on obtient 5, 9 + 4 on obtient 13. Par conséquent, nous obtenons les nombres alternatifs de la série ! Si on additionne les carrés, on obtient -
1 + 1 = 2
1 + 1 + 4=6
1 + 1 + 4 + 9 = 15 ,et ainsi de suite.
Donc 2 = 1 * 2, 6 = 2 * 3, 15 = 3 * 5 et ces facteurs entrent dans la série de Fibonacci !
Maintenant, il y a une raison pour laquelle ces modèles sont formés. Nous savons que -
1^1 + 1^1 + 2^2 + 3^2 + 5^2 = 40 = 8 × 5
Si on le met dans une grande boîte comme celle qui est donnée ci-dessous et qu'on trouve la surface, qu'est-ce qu'on obtient ? Nous obtenons la série ci-dessus !

Si on divise le deuxième nombre par le premier à partir de 8, par exemple-
104 = 13 * 8
273 = 13 * 21
13 ÷ 8 = 1.625
21 ÷ 13 = 1.615
34 ÷ 21 = 1.619
et le nombre d'or ou phi est d'environ 1,618 ! Phi ou le nombre d'or est un nombre très spécial. Ceux qui ont lu "Da Vinci Code" en ont certainement entendu parler. Phi est visible partout. Les espaces entre les yeux et le blanc des yeux sont en proportion dorée, le rapport entre votre avant-bras et votre main est en proportion dorée, les spirales de l'ADN sont en proportion phi, les têtes de graines au centre d'un tournesol et cette liste peut continuer à l'infini.
Source d'Image:
Images de Google (Image du lapin)
Translated to French by Samantha Donato





